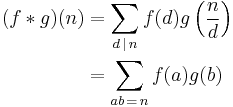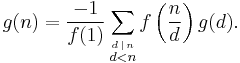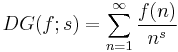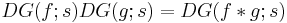Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.
Contents |
Definition
If ƒ and g are two arithmetic functions (i.e. functions from the positive integers to the complex numbers), one defines a new arithmetic function ƒ * g, the Dirichlet convolution of ƒ and g, by
where the sum extends over all positive divisors d of n, or equivalently over all pairs (a, b) of positive integers whose product is n.
Properties
The set of arithmetic functions forms a commutative ring, the Dirichlet ring, under pointwise addition (i.e. f + g is defined by (f + g)(n)= f(n) + g(n)) and Dirichlet convolution. The multiplicative identity is the function  defined by
defined by  (n) = 1 if n = 1 and
(n) = 1 if n = 1 and  (n) = 0 if n > 1. The units (i.e. invertable elements) of this ring are the arithmetic functions f with f(1) ≠ 0.
(n) = 0 if n > 1. The units (i.e. invertable elements) of this ring are the arithmetic functions f with f(1) ≠ 0.
Specifically, Dirichlet convolution is[1] associative,
- (f * g) * h = f * (g * h),
distributes over addition
- f * (g + h) = f * g + f * h = (g + h) * f,
is commutative,
- f * g = g * f,
and has an identity element,
- f *
 =
=  * f = f.
* f = f.
Furthermore, for each f for which f(1) ≠ 0 there exists a g such that f * g =  , called the Dirichlet inverse of f.
, called the Dirichlet inverse of f.
The Dirichlet convolution of two multiplicative functions is again multiplicative, and every multiplicative function has a Dirichlet inverse that is also multiplicative. The article on multiplicative functions lists several convolution relations among important multiplicative functions.
Given a completely multiplicative function f then f (g*h) = (f g)*(f h), where juxtaposition represents pointwise multiplication.[2] The convolution of two completely multiplicative functions is a fortiori multiplicative, but not necessarily completely multiplicative.
Examples
In these formulas
 is the multiplicative identity. (I.e.
is the multiplicative identity. (I.e.  (1) = 1, all other values 0.)
(1) = 1, all other values 0.)- 1 is the constant function whose value is 1 for all n. (I.e. 1(n) = 1.) Keep in mind that 1 is not the identity.
- 1C, where
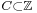 is a set is the indicator function. (I.e. 1C(n) = 1 if n ∈ C, 0 otherwise.)
is a set is the indicator function. (I.e. 1C(n) = 1 if n ∈ C, 0 otherwise.) - Id is the identity function whose value is n. (I.e. Id(n) = n.)
- Idk is the kth power function. (I.e. Idk(n) = nk.)
- The other functions are defined in the article arithmetical function.
- 1 * μ =
 (the Dirichlet inverse of the constant function 1 is the Möbius function.) This implies
(the Dirichlet inverse of the constant function 1 is the Möbius function.) This implies
- g = f * 1 if and only if f = g * μ (the Möbius inversion formula).
- λ * |μ| =
 where λ is Liouville's function.
where λ is Liouville's function.
- λ * 1 = 1Sq where Sq = {1, 4, 9, ...} is the set of squares
 k = Idk * 1 definition of the function σk
k = Idk * 1 definition of the function σk
 = Id * 1 definition of the function σ = σ1
= Id * 1 definition of the function σ = σ1
- d = 1 * 1 definition of the function d(n) = σ0
- Idk =
 k *
k *  Möbius inversion of the formulas for σk, σ, and d.
Möbius inversion of the formulas for σk, σ, and d.
- Id =
 *
* 
- 1 = d * μ
- d 3 * 1 = (d * 1)2
 * 1 = Id This formula is proved in the article Euler's totient function.
* 1 = Id This formula is proved in the article Euler's totient function.
- Jk * 1 = Idk
- (IdsJr) * Js = Js + r
 =
=  * d Proof: convolve 1 to both sides of Id =
* d Proof: convolve 1 to both sides of Id =  * 1.
* 1.
- Λ * 1 = log where Λ is von Mangoldts' function
Dirichlet inverse
Given an arithmetic function ƒ its Dirichlet inverse g = ƒ−1 may be calculated recursively (i.e. the value of g(n) is in terms of g(m) for m < n) from the definition of Dirichlet inverse.
For n = 1:
- (ƒ * g) (1) = ƒ(1) g(1) =
 (1) = 1, so
(1) = 1, so
- g(1) = 1/ƒ(1). This implies that ƒ does not have a Dirichlet inverse if ƒ(1) = 0.
For n = 2
- (ƒ * g) (2) = ƒ(1) g(2) + ƒ(2) g(1) =
 (2) = 0,
(2) = 0, - g(2) = −1/ƒ(1) (ƒ(2) g(1)),
For n = 3
- (ƒ * g) (3) = ƒ(1) g(3) + ƒ(3) g(1) =
 (3) = 0,
(3) = 0, - g(3) = −1/ƒ(1) (ƒ(3) g(1)),
For n = 4
- (ƒ * g) (4) = ƒ(1) g(4) + ƒ(2) g(2) + ƒ(4) g(1) =
 (4) = 0,
(4) = 0, - g(4) = −1/ƒ(1) (ƒ(4) g(1) + ƒ(2) g(2)),
and in general for n > 1,
Since the only division is by ƒ(1) this shows that ƒ has a Dirichlet inverse if and only if ƒ(1) ≠ 0.
Dirichlet series
If f is an arithmetic function, one defines its Dirichlet series generating function by
for those complex arguments s for which the series converges (if there are any). The multiplication of Dirichlet series is compatible with Dirichlet convolution in the following sense:
for all s for which both series of the left hand side converge, one of them at least converging absolutely (note that simple convergence of both series of the left hand side DOES NOT imply convergence of the right hand side!). This is akin to the convolution theorem if one thinks of Dirichlet series as a Fourier transform.
Related Concepts
The restriction of the divisors in the convolution to unitary, bi-unitary or infinitary divisors defines similar commutative operations which share many features with the Dirichlet convolution (existence of a Möbius inversion, persistence of multiplicativity, definitions of totients, Euler-type product formulas over associated primes,...).
References
- ^ Proofs of all these facts are in Chan, ch. 2
- ^ A proof is in the articleCompletely_multiplicative_function#Proof_of_pseudo-associative_property.
- Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR0434929
- Chan Heng Huat (2009). Analytic Number Theory for Undergraduates. World Scientific Publishing Company. ISBN 9814271365.
- Hugh L. Montgomery; Robert C. Vaughan (2007). Multiplicative number theory I. Classical theory. Cambridge tracts in advanced mathematics. 97. Cambridge: Cambridge Univ. Press. p. 38. ISBN 0-521-84903-9.
- Cohen, Eckford (1959). "A class of residue systems (mod r) and related arithmetical functions. I. A generalization of Möbius inversion". Pacific J. Math. 9 (1): pp. 13—23. MR0109806.
- Cohen, Eckford (1960). "Arithmetical functions associated with the unitary divisors of an integer". Mathematische Zeitschrift 74: pp. 66—80. doi:10.1007/BF01180473. MR0112861.
- Cohen, Eckford (1960). "The number of unitary divisors of an integer". American mathematical monthly 67 (9): pp. 879—880. MR0122790.
- Cohen, Graeme L. (1990). "On an integers' infinitary divisors". Math. Comp. 54 (189): pp. 395—411. doi:10.1090/S0025-5718-1990-0993927-5. MR0993927.
- Cohen, Graeme L. (1993). "Arithmetic functions associated with infinitary divisors of an integer". Intl. J. Math. Math. Sci. 16 (2): pp. 373—383. doi:10.1155/S0161171293000456.
- Sandor, Jozsef; Berge, Antal (2003). "The Möbius function: generalizations and extensions". Adv. Stud. Contemp. Math. (Kyungshang) 6 (2): 77–128. MR1962765.
- Finch, Steven (2004). "Unitarism and Infinitarism". http://algo.inria.fr/csolve/try.pdf.